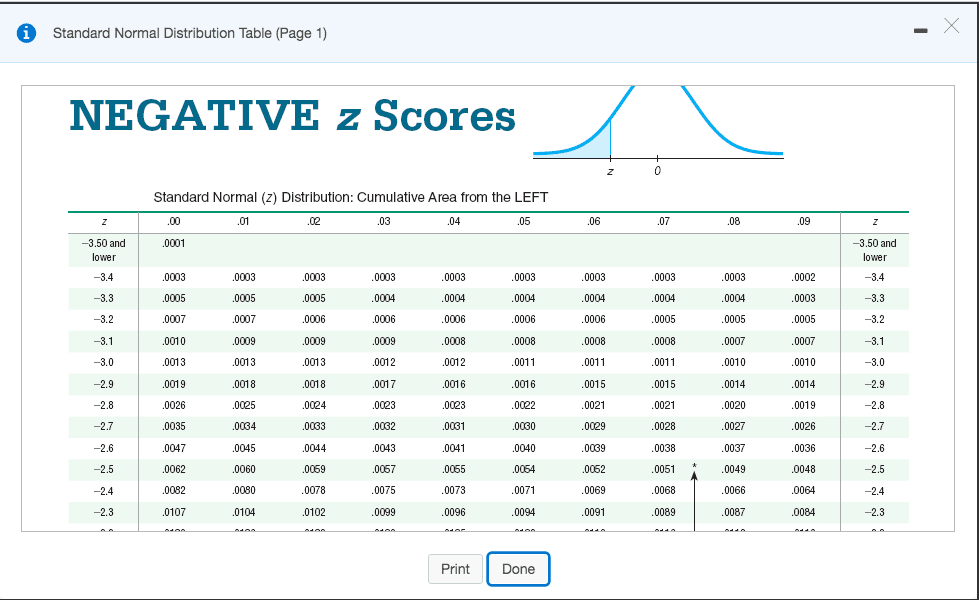
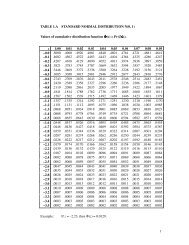
This forms the second part of the z-score. This time, the value on the x-axis for 0.8997 is 0.08.
We now need to do the same for the x-axis, using the 0.8997 value as our starting point and following the column up. You will notice that the value on the y-axis for 0.8997 is 1.2. If we take the 0.8997 value as our starting point and then follow this row across to the left, we are presented with the first part of the z-score. When looking at the table, you may notice that the closest value to 0.9 is 0.8997.
As such, we first need to find the value 0.9 in standard normal distribution table. We know the percentage we are trying to find, the top 10% of students, corresponds to 0.9.